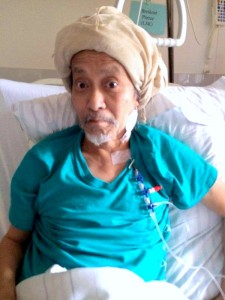
Hi, I didn’t contact you for quite a while.
I didn’t inform you that I’m ill.
Stayed three months in hospital for very difficult operation.
No worries hard period is gone, I’m getting everyday better,
So, I had to cancel scheduled shows.
I don’t know when I’m able to back on the road again where I feel most comfortable.
I might don’t see you for long time.
But, I’ll back.
Wish you every good thing come and happen and make you happy in year 2015!
Feel Free Energy!
Damo Suzuki //
Get well soon Damo….Energy!
Get well soon Damo. Looking forward to seeing you do what you do best again soon. x
Wishing you warm wishes. Take life easy Damo . Hope to see you when your energy is right…X
Get well soon Damo, spring focus and delightful realities. xxx
Damo,
Is there an email to reach you? I wish to extend my love and support for you but find these replies too public.
Sincere best wishes Damo, strength and energy and wishing you a full recovery soon. Mark
Hi, Damo! Have a wonderful birthday. Get well soon! All music lovers miss you so much! <3
I’m sending you all my love Damo!!! Happy Happy Birthday and see you soon:)))
Patrycja
xxxx
Wishing you well & good health. Peace from a new fan. All the best from me to you.
alles gute für Dich lieber Damo – get well soon – wir sehen uns hoffentlich bald mal wieder – grüsse – D
gute besserung + komm zurück auf die bühne (und ins studio), damit wir weiterhin deine gute, verrückte musik hören + erleben können. aus Berlin. all the best Sea Wanton
Hang in there Damo. We love you brother !! Here’s to a healthy 2015.
Karl
We love you, Damo 🙂
Get well soon!
Very best wishes Damo! Get well soon!
Gordon,
Thanks for your mail, I’m getting better day by day and hope to see you in further!
Energy!
Damo@Cologne
Sad to hear this news Damo, but happy you are getting better.
Rest & recover!
🙂
Have a brilliant 2015.
Best wishes and get well soon! On behalf of all the Hebden Bridge sound carriers.
Wishing you a speedy recovery.
Love from Ned, Gena, Otis & Willow in Hebden Bridge
Stay strong. And take your time.
Hope recovery continues to go well! Much good energy to you, from the Hebden Bridge Netherwoods!
Hi Damo
I really wish you well and hope to see you in London. I’ve been battling an illness for the past 7-8 months and, as I’m sure you know, mental state plays a HUGE role on your recovery. Didn’t you call yourself a spiritual nomad? Here’s another journey for you!
See you in London and best wishes for 15
Thanks.
You too get healthy.
Didn’t have been London for while. When I’m able to travel, London is one of most easiest place to perform. Also within one hour I’ll be there.
Energy!
Damo@Cologne
GET WELL SOON DAMOOO!!!!!
HELLO FROM MILAN!
WE ARE WAITING TO SEE YOU BACK ON STAGE
BEST WISHES
TOBIA
Tobia,
To get back spiritual standard and con dition before operation.
My foods are reading books, watching good movies, eating self-made home cooking.
Dreaming Milano…my movie begging with huge amazing museum like giant central station…. I’ve many good friends there, it’s not easy to find main actor, but it doesn’t matter everybody is an actor
Yes
You have my email!
write me if you want to come to Milan! You are most welcome in my place!
Take care of yourself
<3
Get well soon Damo!
Matt,
Thanks for your message.
Yesterday, I walked through park for around 90 minutes.
This is the longest stretch I ever done since my illness.
After I was so tired but, happy.
You see I’m getting back my old condition soon.
Energy!
Damo@Cologne
Damo my dear friend from Future Space, several days ago I was listening to the Seattle cd and my recording of my set at the same concert. I have so many happy memories of travelling and playing with you. Much love. I hope to meet you again soon, on a stage!
Mark and Elaine Spybey x
Mark,
Can remember Andrew whom you introduce me for place to stay in Edinburgh few years ago? We became friend. We met many times in Edinburgh and London (where he works now) He was visiting Cologne to expedition carnival last week. We’re talking about you and wondered what you’re doing.
Energy!
Damo@Cologne
Damoさん
We miss you!
I want to see you!!
Damo, I hope every day you feel a little stronger & it won’t be too long before we see & hear you sing again.
Best Wishes,
Flowboy
Robin,
I’m getting better day by day for sure.
Just I have to concentrate get best condition.
I’m a fighter all of my life.
The day will come see out side of this tunnel….
Energy!
Damo@Cologne
Wishing you a complete recovery, lots of free energy and plenty of happiness this year.
Sheer,
I’ll wash myself and will go out for walk.
Birds are singing a beautiful day.
Everything I see and feel are enjoyable.
Like fresh morning, your brain is not planed yet.
You have world of your own.
Any thing to come as challenge is just time to learn.
Yes, I’m charging much energy.
Energy!
Damo@Cologne
am praying for early recovery! please come back truly to perform in future days.
Thanks for your message Hideko,
It will be long way, me to get recover.
But, there are many warm messages to me, this will give me power to walk.
At yet, I’m not possible to travel alone anywhere.
My alternative now is watching DVDs and reading books. For some creative thing, no ambition to continue….Maybe I’m too lazy.
Energy!
Damo@Cologne
Hi Damo,
Wishing you a smooth recovery!
Many a night while I was working away on my art or trying to reconnect with that feeling that inspires us to create, you were singing away in the background.
Thank you!
sending love-filled light to Cologne to brighten the days for you. May you enjoy every one of them to the fullest and recover soon.
Alexandra,
Light will be 7 colours of rainbow.
The Sign of hope.
Cover this planet.
Energy!
Damo@Cologne
Wishing you a speedy recovery and good health in 2015. Stay well & take care, Damo! Len Del Rio (Anubian Lights)
Len, Old friend
Thanks for your message.
Whenever you visit Europe, shout me we have to meet up since long time.
I’m getting better but unfortunately I’ve got gout last days.
A sunshine day, it’s pity not able to out.
But, I’m on better way for sure.
Energy!
Damo@Cologne
Damo, so sorry to find out you have been ill. I wish you love and strength for your recovery.
Geoff,
Thanks for your message.
Everyday different condition, Like climbing mountain up and down.
Wish I can touch cloud very soon….
Energy!
Damo@Cologne
Damo, I came of age in Memphis, Tennessee in the early 80’s and was lucky to have a friend who turned me on to your music. I still have those records. Sadly, I missed you when you performed in Memphis a few years ago-I can’t believe I didn’t know you were coming. Now I am fortunate to live not far from you in Essen and am waiting patiently for your triumphant return! Just curious -which local musicians do you like to see and hear? Be well. Sun. Eric.
Eric,
That’s good you moved to old Europe.
So, there will much possibility for you to visit Network performance as I won’t go to States.
At yet I’m not able to, but it will be change.
It’s quote long time ago, I performed in Memphis.
I cannot remember quite well.
There’s quite good sound carriers here in Germany.
You can visit my website click „link“ then you may find sound carriers I’m meaning.
By the way what made you move to Essen?
Energy!
Damo@Cologne.
love your music, and wishing you eine gute besserung!
Bruce,
I feel good like weather of today….sunshine day!!!!
Lay in garden for 2 hours.
I look so healthy brown like just come back from holiday in South.
Energy!
Damo@Cologne
All the best Damo. Wish you a speedy recovery, and take time…
John,
Thank you, I’ll get my self back and on the road again.
Energy!
Damo@Cologne
Damo, I just dug out a recording of us and many unique sound carriers (new friends that night!) at the Ruby Lounge (Manchester 2009). I just checked in to your site to see how you are doing, to find out you have been ill. I am glad you are on the mend. We have shared some great times over ten years ! Love and positivity Steve and Kathy Dinsdale xxx
Steve,
Last time we met was in Sheffield, I guess two years ago.
I’ve forced holiday for already 10 months.
This is also experience that I can learn something.
Fortunately, we had historical heat summer this part of Europe that I can feel like holiday ever I have to stay at home.
Energy!
Damo@Cologne
Steve
I played with you that night! It came to mind this morning and I searched to see if there was any record of it out there and found this thread. I’d love to hear it
americanwrestlers@gmail.com
best
Gary
my beloved Damo!! I wish you health and harmony, I send my best wishes to you!I am sure that you will be more powerfull than before the illness!!!! All my love from ATHENS GREECE your friend and sound carrier Tilemachos Moussas!
Thanks, Tilemachos!
I’m almost out of long tunnel, see slowly light.
I have to be a patient.
By the way I’m preparing tour from May next year onward.
Have a nice day!
Energy!
Damo@Cologne